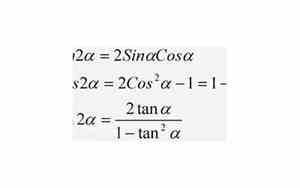
"cos(2x)" 是余弦函数的二倍角公式，它表示的是角x的两倍的余弦值。在三角学中，这个公式可以进一步展开为：

\[ \cos(2x) = \cos^2(x) - \sin^2(x) \]

这个公式利用了著名的和差化积公式，其中 \(\cos(2x)\) 可以通过角x的余弦和正弦的平方和差来表达。这是因为在直角三角形中，如果一个角是2x，那么它的余弦值可以看作是邻边与斜边的比例，而正弦值是对边与斜边的比例。当把这个角度分成两个x时，平方和差的形式就产生了。

若需要展开式中的进一步简化，比如在某些特定角度时，比如 \(x = \frac{\pi}{4}\) 或 \(x = \frac{\pi}{2}\)，则会有特定的值，比如。

cos2x等于什么怎么推导

"cos(2x)" 的推导源自三角函数的和差公式，尤其是二倍角公式。这个公式是基于三角形中的基本关系以及几何性质推导出来的。

我们知道余弦函数 \( \cos(2x) \) 表示一个顶角为2x的等腰直角三角形的邻边与斜边的比例。这个直角三角形可以分为两个相等的45度角三角形，每个角为 \( x \)。

1. 假设顶角为 \( 2x \)，则两个45度角的余弦值分别是 \( \cos(x) \)。现在，直角三角形的两个45度角的余弦值相等，等于 \( \frac{\sqrt{2}}{2} \)（因为 \( \cos(45^\circ) = \frac{\sqrt{2}}{2} \)）。

2. 当我们将这两个小的45度角的三角形拼接在一起，斜边（原三角形的斜边）会是相邻两个小三角形斜边的和（两个 \( \frac{\sqrt{2}}{2} \) 的和），而邻边（原三角形的邻边）会是两个小三角形邻边的乘积，即 \( \cos(x) \cdot \cos(x) = \cos^2(x) \)。

3. 所以，整个大三角形的余弦值 \( \cos(2x) \) 就是这个邻边和斜边的比例，即 \( \cos^2(x) \) 除以 \( \sqrt{2} \) 的平方，也就是 \( \cos^2(x) \)。但这还不是全部，因为还有缺少的另一半，即正弦的平方，因为这是45度角三角形的对边和斜边的比值，即 \( \sin^2(x) \)。

4. 结合相等的两个45度角，我们得到：
\[ \cos(2x) = \cos^2(x) - \sin^2(x) \]

这就是 \( \cos(2x) \) 的基本公式，它是三角恒等式的一个重要成员。这个推导基于角度相加的原理，即 \( \cos(A + B) \) 的形式，但在这里我们特化为 \( A = B = x \)。

cos2x等于什么三角公式

\( \cos(2x) \) 等于一个特定的三角公式，它是二倍角的余弦公式，也称为余弦的复合角公式。这个公式是：

\[ \cos(2x) = \cos^2(x) - \sin^2(x) \]

这个公式是基于三角函数的和差公式，其中 \( \cos(A + B) \) 可以分解为 \( \cos(A)\cos(B) - \sin(A)\sin(B) \)，当 \( A = B \) 时，也就是 \( A = 2x \) 时，\( B \) 同样为 \( 2x \)，上述公式就简化为 \( \cos(2x) = \cos^2(x) - \sin^2(x) \)。

这个公式在解决涉及二倍角的三角问题时非常有用，因为它可以将复杂的二倍角问题转化为只包含 \( x \) 的基本三角函数。在直角三角形中，这个公式揭示了邻边与斜边的关系，或者说，它体现了等腰三角形中两个45度角的特性。

cos2x等于什么万能公式

"万能公式"通常是指泰勒公式在三角函数中的应用，特别是余弦函数 \( \cos(x) \) 的泰勒展开式。但提到 \( \cos(2x) \)，我们通常讨论的并不是一个完整的"万能公式"，因为每个 \( n \) 次多项式级数对于 \( \cos(2x) \) 都有其特定的展开形式，最常见的是二倍角公式我刚才提到的：

\[ \cos(2x) = \cos^2(x) - \sin^2(x) \]

如果我们要考虑泰勒公式，它通常是一个无限级数，对于 \( \cos(2x) \)，我们可以写出：

\[ \cos(2x) = \sum_{n=0}^{\infty} \frac{(-1)^n(2x)^{2n}}{(2n)!} = 1 - 2x^2 + \frac{2x^4}{2!} - \frac{2x^6}{4!} + \cdots \]

这是 \( \cos(2x) \) 在 \( x \) 的无穷级数展开，但这并不是一个"万能公式"，因为实际应用中我们通常只取有限项，比如取到 \( x^2 \) 或 \( x^4 \) 级的项，这取决于问题的具体需求和精确度要求。