sin求导等于什么

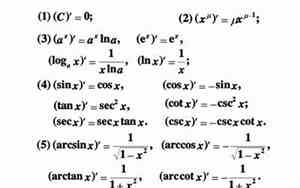
求导是微积分中的一个基本概念，它用于找出函数的瞬时变化率。对于三角函数中的正弦函数 \(\sin x\)，其导数可以直接使用求导规则得出。

根据基本求导法则，如果 \(y = \sin x\)，其导数 \(y' = \frac{dy}{dx}\) 可以通过应用链式法则来计算，因为 \(\sin x\) 可以看作是 \(x\) 通过三角函数映射得到的。对于 \(\sin x\)，其导数是 \(\cos x\)，因为 \(\cos x\) 是 \(\sin x\) 关于 \(x\) 的导数。所以：

\[
\frac{d}{dx}[\sin x] = \cos x
\]

所以 \(\sin x\) 的导数就是 \(\cos x\)。

cos和sin求导

对于余弦函数 \(\cos x\) 和正弦函数 \(\sin x\)，它们的导数是它们自身的周期性倒数：

1. 对于 \(\cos x\)，其导数是 \(-\sin x\)。这是因为 \(\cos x\) 是 \(\sin x\) 的减函数，所以它的变化率是负的。数学上，你可以这样表达：
\[
\frac{d}{dx}[\cos x] = -\sin x
\]

2. 对于 \(\sin x\)，我们已经知道它的导数是 \(\cos x\)，因为我们在之前提到过：
\[
\frac{d}{dx}[\sin x] = \cos x
\]

这些导数在许多数学问题中都有应用，比如在解决三角函数的微分问题、解析函数的导数性质，或者周期函数的周期分析等。

sin求导公式推导

正弦函数 \(\sin x\) 的导数可以通过泰勒级数或者微分的概念来推导。下面是两种主要的推导方法：

1. 泰勒级数法：
\(\sin x\) 是一个周期函数，其在 \(x=0\) 点的泰勒级数展开式为：
\[
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots
\]
对于任意的 \(x\)，每一项都是 \(x\) 的幂次乘以一个系数。导数就是泰勒级数中每一项系数的乘积，但系数都会减少一个指数。因此，当 \(x\) 的幂次增加时，它的系数将变为负，使得奇数次项与偶数次项相互抵消。所以，从展开式中去除 \(x\) 的幂次项，我们可以看到：
\[
\frac{d}{dx}[\sin x] = \cos x
\]
因为仅剩下的是一阶项 \(\frac{x^1}{1!} = x\) 的系数，即常数项，是 \(\cos x\)。

2. 利用三角恒等式和求导规则：
你可以直接使用三角函数的基本导数规则，它是基于三角函数定义的自然导数。因为 \(\sin x\) 的定义是单位圆上的点与原点连线的正向切线，所以它的变化率是指向单位圆的半径，即 \(\cos x\)，这也符合单位圆上相邻两个角度（一个为 \(x\)，一个为 \(x + \pi\)）的切线关系。

两种方法得出的结果都是一致的：\(\sin x\) 的导数是 \(\cos x\)。这是三角函数正弦和余弦之间基本关系的一个重要体现。

sin求导变cos是正还是负

当求 \(\sin x\) 的导数时，根据导数的定义，导数表示的是函数在某一点处的变化率。对于 \(\sin x\)，它的导数是 \(\cos x\)，这是因为 \(\sin x\) 的单位圆图像上，每一点的切线斜率是垂直于该点的长度，即对应的角度的余弦值。所以，不论 \(x\) 的具体取值如何，\(\sin x\) 在每个点的导数都是 \(x\) 的余弦值，即 \(\cos x\)，而 \(\cos x\) 本身是周期为 \(2\pi\) 的，它在 \(0\) 到 \(\pi\) 之间是正的，在 \(\pi\) 到 \(2\pi\) 之间是负的（因为余弦是 \(-1\) 到 \(1\) 之间的周期函数）。

总结来说，\(\sin x\) 的导数 \(\cos x\) 是正的，但这取决于 \(x\) 的具体范围。如果你想知道某个具体 \(x\) 值的导数是正还是负，需要根据 \(x\) 的实际值来判断 \(\cos x\) 的符号。