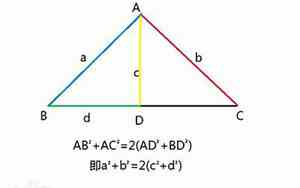
在初中数学中，三角形的中线通常指的是从一个顶点出发，连接对边中点的线段。对于任意一个三角形ABC，如果从顶点A向BC边的中点D画一条中线，其长度公式可以通过等腰三角形的性质来计算，因为AD这条中线会将原三角形ABC分成两个等腰三角形。

具体公式如下：
设AD是中线，AB和AC是三角形的两边，那么AD的长度（D是BC的中点）为：
\[ AD = \frac{1}{2} BC \]

这是一个基础的等腰三角形性质，不需要复杂的几何证明。如果要知道中线AD与原三角形某边的关系，例如AD与AB，可能需要知道具体的比例或者角度关系，或者使用相似三角形的性质进行计算。

但请注意，如果没有额外信息，通常的中线长度就是它所对边的一半。如果需要解决更复杂的三角形中线问题，可能涉及到三角函数或者面积相关的内容，这就需要更多的条件和知识了。如果你遇到了具体的题目，欢迎提供详细信息，我会为你提供更精确的解答。

三角形中线长度公式推导向量法证

向量法是一种更高级的数学工具，尤其在处理几何问题时，它能够简化证明过程。对于三角形中线长度的向量证明，我们通常利用向量的加减和点的坐标来阐述。

假设三角形ABC中，AD是BC边的中线，A、B、C三点的坐标分别为\( A(a_x， a_y) \)， \( B(b_x， b_y) \)， \( C(c_x， c_y) \)，则点D的坐标是\( B \)和\( C \)坐标的平均值，即\( D(\frac{b_x + c_x}{2}， \frac{b_y + c_y}{2}) \)。

向量\( \overrightarrow{AD} \)可以用A点和D点的坐标差表示，即：
\[ \overrightarrow{AD} = \overrightarrow{AD} = D - A = \left(\frac{b_x + c_x}{2} - a_x， \frac{b_y + c_y}{2} - a_y\right) \]

由于D是BC边的中点，向量\( \overrightarrow{BD} \)和\( \overrightarrow{CD} \)的和等于\( \overrightarrow{BC} \)，所以：
\[ \overrightarrow{BD} + \overrightarrow{CD} = \overrightarrow{BC} \]
\[ \left(\frac{b_x - a_x}{2}， \frac{b_y - a_y}{2}\right) + \left(\frac{c_x - a_x}{2}， \frac{c_y - a_y}{2}\right) = (c_x - b_x， c_y - b_y) \]

将向量相加后，我们看到每个分量都是边BC的长度的一半，因此：
\[ \overrightarrow{AD} = \left(\frac{1}{2}(c_x - b_x)， \frac{1}{2}(c_y - b_y)\right) \]

这与公式 \( AD = \frac{1}{2} BC \) 相一致，反映出中线长度是它所对边的一半。这就是使用向量法证明三角形中线长度的基本方法。但请记住，向量法通常适用于有明确坐标或向量表达的几何问题。

三角形中线长度公式证明方法

三角形中线长度的证明方法通常有几种，下面我将介绍两种常见的证明方法：

1. 几何证明（不涉及向量法）:
基础证明：
假设\( AD \)是三角形\( ABC \)中BC边的中线，那么\( D \)是\( BC \)的中点。连接\( A \)到\( BC \)的中点\( D \)，就知道\( AD \)是\( \Delta ABC \)等腰三角形\( ADC \)的一部分，因为\( AD \)是底边的一半。所以\( AD = \frac{1}{2} BC \)。

三角形面积法：
如果知道三角形的面积公式 \( A = \frac{1}{2} \times 底 \times 高 \)，可以先计算出\( \Delta ABD \)和\( \Delta ADC \)的面积，两者的和等于\( \Delta ABC \)的面积，由于\( D \)是中点，所以\( AB \)和\( AC \)的高相等，因此\( AD \)就是两部分高的和，即\( AD = \frac{1}{2} BC \)。

2. 向量法:
向量法需要知道每个顶点的坐标。设A，B，C分别是三个顶点的坐标，\( \overrightarrow{AD} \)是中线的向量。由于D是BC的中点，\( \overrightarrow{AD} \)等于\( \overrightarrow{AB} + \overrightarrow{AC} \)的一半，即\( \overrightarrow{AD} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) \)。
接下来，可以通过向量的线性关系，\( \overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{CB} \)，将\( \overrightarrow{AD} \)表示为\( \frac{1}{2}(\overrightarrow{AC} + \overrightarrow{CB}) \)，简化后得到\( AD = \frac{1}{2} BC \)。

这两种方法都是基于中线将三角形分成两个等底等高的部分这一性质。如果你需要更详细或特定的证明，或者有其他问题，请随时提问。