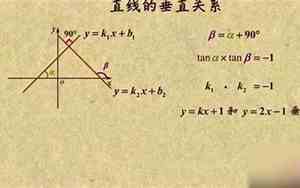
两条直线垂直的条件是它们的斜率具有特定的关系。在直角坐标系中，如果直线\( l1 \)的斜率是\( m1 \)，直线\( l2 \)的斜率是\( m2 \)，那么这两条直线垂直的斜率关系是\( m1 \times m2 = -1 \)。

证明：

证明两点垂直的几何方法是使用两条直线的斜率定义。若一条直线的斜率\( m1 \)可以用一般式\( y = mx + c \)表示，其中\( m \)是斜率，\( c \)是y轴截距。对于垂直线，其斜率不存在，或者说等于无穷大，记作\( m2 = \infty \)（实际上，垂直线的斜率为不存在的特殊表示）。当两条直线垂直时，一条直线的斜率乘以另一条的斜率得到的结果等于-1。

我们可以将两条直线的垂直关系写成比例的形式：
\[ m1 \times m2 = \frac{\Delta y}{\Delta x} \times \frac{\Delta y}{\Delta x} = \left(\frac{-1}{1}\right) = -1 \]

这表明不论两条直线的具体斜率是多少，只要它们是垂直的，它们的乘积总是等于-1。这就是两条垂直线斜率关系的数学证明。

两条垂直线的斜率有什么关系

两条垂直线的斜率具有特定的关系：它们的斜率之积为-1。在直角坐标系中，如果直线A的斜率为\( m_A \)，而直线B垂直于直线A，那么直线B的斜率记为\( m_B \)，则有：

\[ m_A \times m_B = -1 \]

这个关系成立的原因是斜率是直线倾斜程度的度量，垂直线意味着它们的倾斜角度正好是90度，而90度的正切值是无定义的，用数学符号表示就是不存在，通常用无穷大或斜率不存在来表示。在这种情况下，直线A的斜率乘以无穷大或不存在的斜率，等于-1。这是垂直线斜率关系的基本性质。

两条线垂直斜率怎么样

两条线垂直时，它们的斜率之间存在一个特定的关系。如果直线A的斜率为\( m_A \)，而直线B垂直于直线A，那么直线B的斜率记为\( m_B \)，根据垂直线的性质，两条线的斜率乘积为-1，即：

\[ m_A \times m_B = -1 \]

这意味着，如果直线A的斜率不为0（因为垂直线的斜率通常表示为不存在，我们用0的倒数来代替，记为无穷大或不存在），那么直线B的斜率将是直线A的斜率的负倒数。例如，如果直线A的斜率为3，那么直线B的斜率就是\( \frac{-1}{3} \)。这是几何学中确定两条线是否垂直的标准方法。

两条线垂直斜率公式是什么

两条线垂直的数学公式可以表示为它们的斜率之积等于-1。如果设直线A的斜率为\( m_A \)，而与直线A垂直的直线B的斜率为\( m_B \)，则：

\[ m_A \times m_B = -1 \]

这说明无论直线A的斜率是什么值，只要直线B与A垂直，其斜率就是A的斜率的负倒数。例如，如果直线A的斜率为3，那么直线B的斜率就是\( -\frac{1}{3} \)。这条公式直接反映了垂直线的性质，即它们的方向是完全相反的，与正交相吻合。

两条线垂直斜率相乘等于多少

如果两条线垂直，它们的斜率相乘的结果是-1。这是一个固定的数学关系，无论两条线的具体斜率是多少，只要它们相互垂直，根据这个规则，它们的斜率乘积总是等于-1。例如，如果直线A的斜率为3，而与之垂直的直线B的斜率为\( -\frac{1}{3} \)，它们相乘就是：

\[ 3 \times \left(-\frac{1}{3}\right) = -1 \]

这就是垂直线斜率的基本性质。