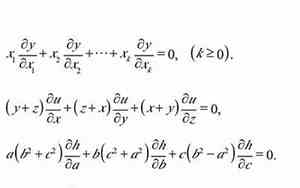
偏微分方程（Partial Differential Equations，PDEs）是数学中的一个核心分支，主要用于描述自然界中许多复杂现象，如流体动力学、电磁学、热传导、波动理论等。它们涉及多个变量并对这些变量的导数求解，因此在理论和应用上都具有一定的复杂性。

对于初学者来说，偏微分方程可能会显得挑战性，因为它们需要更高级的数学工具，如变分法、泛函分析、微分几何等。学习过程中，需要掌握偏导数、解空间概念、特征线方法、分离变量法等基础解题技巧。特别是非线性偏微分方程，它们的解析解往往非常罕见，通常需要数值方法来求解。

一旦掌握了基本原理和技巧，偏微分方程也有其美妙和实用性。它们在科学与工程领域有着广泛的应用，解决了很多实际问题。因此，困难与乐趣并存，对于对数学有热情并愿意投入时间和努力的人来说，挑战是可以克服的。学习过程中，通过逐步深入和实践练习，你会逐渐发现其内在的规律和解决问题的乐趣。

偏微分方程和常微分方程的区别

偏微分方程（Partial Differential Equations， PDEs）和常微分方程（Ordinary Differential Equations， ODEs）是数学中的两大类型，它们的主要区别在于所涉及的未知函数及其依赖关系。

1. 未知函数的变量数：
PDEs 的未知函数通常依赖于多个自变量，如时间与空间（x， y， z），例如温度场、流体速度等。涉及到的导数不止一阶，涉及到了多变量的导数。
ODEs 则仅依赖一个自变量，如时间，未知函数的一阶导数即为其速度或变化率。

2. 求解空间：
PDEs 的解空间通常不是单个数值，而是多维的函数空间。解可能是一个函数，而不仅仅是一个特定的数值点。
ODEs 的解通常是一个一维曲线或者一个数值点的序列，表现为函数在某一自变量上的值。

3. 应用领域：
PDEs 主要用于描述自然界中连续介质的物理现象，如波动、扩散、电磁场等。
ODEs 则更常见于描述孤立系统的动力学行为，如牛顿的运动定律或欧拉-拉格朗日方程。

4. 求解方法：
PDEs 的求解通常更复杂，涉及线性化、傅立叶变换、分离变量法、变分法、数值方法等。
ODEs 的求解方法相对简单，可能有解析解（如线性微分方程）或数值解（如欧拉方法、龙格-库塔法）。

PDEs 更侧重于多维空间和连续变化，而 ODEs 更关注一维变化和孤立系统的动态。理解这两种方程是数学分析与应用数学的核心内容。